Electrical theory can be intimidating, especially to mechanical engineers like myself. I got stuck in while I was working on my bachelor’s in mechanical engineering, and I’m happy I did. Mechanical and electrical engineering are complementary to each other. That drill you designed is a lot more attractive with battery power than it is when powered by hand. What about a cocktail mixing robot or a stepper orchestra?
This post is part of a series of educational blog posts where I deal with the basics. I’m covering the basics on electrical theory, physics, Arduino and much more. These are some basic formulas for reference.
What is electricity?
Electricity is all around us, in fact, it is one of the 4 fundamental forces, it powers our houses, cars, and infrastructure. We can use it to improve our lives, to heat our house, 3D print custom parts, or learn about electricity (like on this site). I’ll be talking about applying electrical theory, if you are interested in what electricity is on a physics level, Sparkfun has a very good explanation.
The electricity that we use to power everything is the continuous flow of charge. This is why circuits need to be a closed-loop to be useful, we need a continuous flow to make things work.
Ohm’s law
We describe electricity in 3 variables, Voltage, Current and Resistance. The relationship of these 3 factors is described by Ohm’s law.
![]()
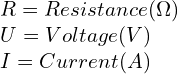
- Voltage is measured in Volts (V) and symbolized in formulas by
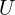
- Current is measured in Amps (A) and symbolized in formulas by
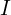
- Resistance is measured in Ohms (Ω) and symbolized in formulas by
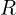
We can rewrite these to produce any of the 3 variables (voltage, current and resistance) like this:
![]()
![]()
You can visualize Ohm’s law as a water reservoir draining. In this visualization, the water level is the voltage, the speed at which the water comes out is the current, and the size of the hole creates resistance.
- With an increase in water level (voltage), the water flow (current) will increase
- With a smaller hole, the resistance will increase, and decrease the flow (current)

Power (Watt)
We measure power in Watt and we use it to describe a large variety of processes. It can be electrical, mechanical, thermal, and because of this, is very useful to describe how much something uses or can produce. The power of a car is usually described in horsepower, but this is very easily converted into Watts (1 horsepower = 745.699872 watts). Power in the realm of electricity is described as factors of voltage and current with the following formula:
![]()
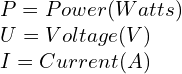
Power can describe the power a motor delivers, but it can also describe how much heat a component produces. The amount of heat any component uses is dependent on the current and the resistance. This next step is an easy one for the math geniuses among us, but I’ll explain it nevertheless. In math there is the substitution rule, this rule says that you can describe any variable by substituting it with the formula that makes it up. This means that we can combine Ohm’s law and the formula for power to describe the influence that current and resistance have on power (and heat production).
In the formula ![]() we can substitute
we can substitute ![]() with the rewritten Ohm’s law
with the rewritten Ohm’s law ![]() to produce:
to produce:
![]()
This says that power a component uses (or produces as heat) has an exponential relationship to current, and a linear relationship to the resistance of that component.
Shortcircuit
A short-circuit occurs when an electrical system has a total resistance that is close to (but not equal to) 0 (zero). I’ll use the above formula’s to explain what happens, and why this generally breaks stuff.
Ohm’s law describing the current a system uses is ![]() shows how much current can flow through a circuit, and the power formula calculates how much power is used/produced in a system. Let’s fill these in with numbers in 2 situations both using a 24V power supply. This is a schematic of this situation:
shows how much current can flow through a circuit, and the power formula calculates how much power is used/produced in a system. Let’s fill these in with numbers in 2 situations both using a 24V power supply. This is a schematic of this situation:
![]() –>
–> ![]()
![]() –>
–> ![]()
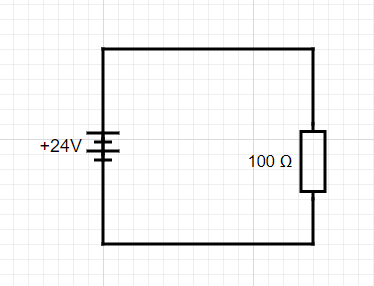
Now the second situation:
![]() –>
–> ![]()
![]() –>
–> ![]()
With the same power supply (24V) we went from a pretty normal situation of 5,76 W (equal to the usage of an RGB computer mouse) to a usage of 5670W, or 5,7kW, or about 3x the maximum current of an average thermal fuse in your house.
Remember kids, short-circuit bad. (unless you mean the movie)
Alternating current (AC) vs direct current (DC)
We use 2 main forms of electricity, AC (alternating current) and DC (direct current). The main difference between these 2 is that AC changes polarity, meaning it goes from positive to negative. As a rule of thumb, AC is used for the power grid, and DC is used to power devices. The reason for this is a little complex, but in essence, it is because DC is very stable and can be easily modulated, and AC makes it very easy to transform the voltage up and down. I will explain the differences and uses of these 2 forms of electricity in an upcoming article.
Stay tuned
Stay tuned for more articles on the basics.
Basic formulas
Ohm’s law![]()
Power![]()
![]()
Kirchoff’s laws![]()
![]()





